❚ Korepetycje z matematyki i fizyki dla uczniów szkół podstawowych klas IV – VIII.
❚ Dojazd do ucznia na terenie Krakowa (+Kryspinów+Liszki+Jeziorzany).
Cena: 100zł / 1h lub 150zł / 2h.
❚ W razie potrzeby możliwość korepetycji przez internet, podczas których korzystam z tabletu graficznego i tablicy online, na której możemy równocześnie pisać.
Cena: 60zł / h.
-
+ Klasy IV – VI
-
+ I. Liczby naturalne w dziesiątkowym układzie pozycyjnym.
- 1. Zapis i odczyt liczb wielocyfrowych.
- 2. Liczby na osi liczbowej.
- 3. Porównywanie liczb.
- 4. Zaokrąglanie liczb.
- 5. Zamiana reprezentacji liczb w zakresie do 3000 z systemu rzymskiego na dziesiątkowy i odwrotnie.
-
+ II. Działania na liczbach naturalnych.
- 1. Dodawanie i odejmowanie w pamięci liczb naturalnych dwucyfrowych lub większych; dodawanie i odejmowanie liczby jednocyfrowej dla dowolnej liczby naturalnej.
- 2. Dodawanie i odejmowanie liczb naturalnych wielocyfrowych sposobem pisemnym i za pomocą
kalkulatora.
- 3. Mnożenie i dzielenie liczby naturalnej przez liczbę naturalną jednocyfrową, dwucyfrową lub trzycyfrową sposobem pisemnym, w pamięci (w najprostszych przykładach) i za pomocą kalkulatora (w trudniejszych przykładach).
- 4. Stosowanie wygodnych dla siebie sposobów ułatwiających obliczenia, w tym przemienności i łączności dodawania i mnożenia oraz rozdzielności mnożenia względem dodawania.
- 5. Porównywanie liczb naturalnych z wykorzystaniem ich różnicy lub ilorazu.
- 6. Rozpoznawanie liczb podzielnych przez 2, 3, 4, 5, 9, 10, 100.
- 7. Rozpoznawanie liczby złożonej, gdy jest ona jednocyfrowa lub dwucyfrowa, a także gdy na istnienie dzielnika właściwego wskazuje cecha podzielności.
- 8. Obliczanie kwadratów i sześcianów liczb naturalnych.
- 9. Reguły dotyczące kolejności wykonywania działań.
- 10. Szacowanie wyników działań.
- 11. Znajdowanie największego wspólnego dzielnika (NWD) i najmniejszej wspólnej wielokrotności (NWW) dwóch liczb naturalnych co najwyżej trzycyfrowych metodą rozkładu na czynniki.
- 12. Rozpoznawanie wielokrotności danej liczby, kwadratów, sześcianów, liczb pierwszych, liczb złożonych.
- 13. Odpowiadanie na pytania dot. liczebności zbiorów różnych rodzajów liczb wśród liczb z pewnego niewielkiego zakresu (np. od 1 do 200 czy od 100 do 1000), gdy liczba w odpowiedzi jest na tyle mała, że wszystkie rozważane liczby uczeń może wypisać.
- 14. Rozkład liczb naturalnych na czynniki pierwsze, co najwyżej trzycyfrowe, w przypadku gdy co najwyżej jeden z tych czynników jest liczbą większą niż 10.
- 15. Wyznaczanie wyniku dzielenia z resztą liczby a przez liczbę b i zapisanie liczby a w postaci
\(a = b \cdot q + r\), gdzie \(0 \leq r < b \).
-
+ III. Liczby całkowite.
- 1. Praktyczne przykłady stosowania liczb ujemnych.
- 2. Interpretacja liczb całkowitych na osi liczbowej.
- 3. Wartość bezwględna.
- 4. Porównywanie liczb całkowitych.
- 5. Proste rachunki pamięciowe na liczbach całkowitych.
-
+ IV. Ułamki zwykłe i dziesiętne.
- 1. Opis części danej całości za pomocą ułamka.
- 2. Ułamek jako iloraz liczb naturalnych oraz iloraz liczb naturalnych jako ułamek zwykły.
- 3. Skracanie i rozszeszanie ułamków zwykłych.
- 4. Sprowadzanie ułamków zwykłych do wspólnego mianownika.
- 5. Przedstawienie ułamka niewłaściwego w postaci liczby mieszanej, a liczby mieszanej w postaci ułamka niewłaściwego.
- 6. Zapisywanie wyrażeń dwumianowanych w postaci ułamka dziesiętnego i odwrotnie.
- 7. Ułamki zwykłe i dziesiętne na osi liczbowej.
- 8. Ułamki dziesiętne skończone w postaci ułamków zwykłych.
- 9. Zamiana ułamków zwykłych o mianownikach będących dzielnikami liczb 10, 100, 1000 itd. na ułamki dziesiętne skończone dowolną metodą (przez rozszerzanie lub skracanie ułamków zwykłych, dzielenie licznika przez mianownik w pamięci, pisemnie lub za pomocą kalkulatora).
- 10. Zapis ułamków zwykłych o mianownikach innych niż dzielniki liczb 10, 100, 1000 itd. w postaci rozwinięcia dziesiętnego nieskończonego, uzysując to w wyniku dzielenia licznika przez mianownik w pamięci, pisemnie lub za pomocą kalkulatora.
- 11. Zaokrąglanie ułamków dziesiętnych do co najwyżej drugiego miejsca po przecinku (zł, gr, m, cm, mm itp.).
- 12. Porównywanie ułamków zwykłych i dziesiętnych.
- 13. Obliczanie liczby, której część jest podana (wyznaczanie całości, której część określono za pomocą ułamka).
- 13. Wyznaczanie liczby, która powstaje po powiększeniu lub pomniejszeniu o pewną część innej liczby.
-
+ V. Działania na ułamkach zwykłych i dziesiętnych.
- 1. Dodawanie, odejmowanie, mnożenie i dzielenie ułamków zwykłych o mianownikach jedno- lub dwucyfrowych, a także liczb mieszanych.
- 2. Dodawanie, odejmowanie, mnożenie i dzielenie ułamków dziesiętnych w pamięci (w przykładach najprostszych), pisemnie (w przypadku gdy ułamki mają razem co najwyżej 6 cyfr różnych od zera) i za pomocą kalkulatora (w przykładach trudniejszych).
- 3. obliczanie wartości wyrażeń arytmetycznych, wymagających stosowania działań arytmetycznych na liczbach całkowitych lub na liczbach zapisanych za pomocą ułamków zwykłych, liczb mieszanych i ułamków dziesiętnych, także wymiernych ujemnych, z uwzględnieniem reguł dotyczących kolejności wykonywania działań, o stopniu trudności nie większym niż w przykładzie:
\[ -\frac{1}{2}:0.25+5.25:0.05-7\frac{1}{2} \cdot \left(2.5-3\frac{2}{3} \right)+1.25.\]
-
+ VI. Elementy algebry.
- 1. Nieskomplikowane wzory, w których występują oznaczenia literowe.
- 2. Używanie oznaczeń literowych nieznanych wielkości liczbowych i zapis prostych wyrażeń algebraicznych na podstawie informacji osadzonych w kontekście praktycznym, np. zapis obwodu trójkąta o bokach: a, a + 2 , b.
- 3. Równania pierwszego stopnia z jedną niewiadomą występującą po jednej stronie równania, np. \( \frac{x-2}{3}=4. \)
-
+ VII. Proste i odcinki.
- 1. Punkt, prosta, półprosta, odcinek.
- 2. Proste, odcinki prostopadłe i równoległe.
- 3. Rysowanie pary odcinków prostopadłych i równoległych.
- 4. Pomiar odcinka z dokładnością do 1 mm.
- 5. Znalezienie odległości punktu od prostej.
-
+ VIII. Kąty.
- 1. Wskazywanie w dowolnym kącie ramion i wierzchołka.
- 2. Pomiar z dokładnością do 1° kątów mniejszych niż 180°.
- 3. Rysowanie kątów mniejszych od 180°.
- 4. Rozpoznawanie kąta prostego, ostrego i rozwartego.
- 5. Porównywanie kątów.
- 6. Kąty wierzchołkowe i przyległe oraz ich własności.
-
+ IX. Wielokąty, koła i okręgi.
- 1. Rozpoznawanie trójkątów ostrokątnych, prostokątnych, rozwartokątnych, równobocznych i równoramiennych.
- 2. Konstruowanie trójkąta o danych trzech bokach i ustalanie możliwości zbudowania trójkąta o zadanych bokach.
- 3. Stosowanie twierdzenia o sumie kątów wewnętrznych trójkąta.
- 4. Umiejętność rozpoznania i nazwania: kwadrat, prostokąt, romb, równoległobok i trapez.
- 5. Znajomość najważniejszych własności kwadratu, prostokąta, rombu, równoległoboku i trapezu, rozpoznawanie figur osiowosymetrycznych i wskazywanie osi symetrii figur.
- 6. Wskazywanie na rysunku: cięciwa, średnica oraz promień koła i okręgu.
- 7. Rysowanie cięciwy koła i okręgu, a także, jeżeli dany jest środek okręgu, promienia i średnicy.
- 8. W trójkącie równoramiennym wyznaczanie przy danym jednym kącie: miary pozostałych kątów; oraz przy danym obwodzie i długości jednego boku – długości pozostałych boków.
-
+ X. Bryły.
- 1. Rozpoznawanie: graniastosłupy proste, ostrosłupy, walce, stożki i kule – w sytuacjach praktycznych i wskazywanie tych brył wśród innych modeli brył.
- 2. Wskazywanie wśród graniastosłupów prostopadłościanów i sześcianów wraz z uzasadnieniem wyboru.
- 3. Rozpoznaje siatki graniastosłupów prostych i ostrosłupów.
- 4. Rysowanie siatki prostopadłościanów.
- 5. Wykorzystywanie podanych zależności między długościami krawędzi graniastosłupa do wyznaczania długości poszczególnych krawędzi.
-
+ XI. Obliczenia w geometrii.
- 1. Obliczanie miary kątów, stosując przy tym poznane własności kątów i wielokątów.
- 2. Obliczanie obwodu wielokąta o danych długościach boków.
- 3. Obliczenia pól: trójkąta, kwadratu, prostokąta, rombu, równoległoboku, trapezu, przedstawionych na rysunku oraz w sytuacjach praktycznych, w tym także dla danych wymagających zamiany jednostek.
- 4. Stosowanie jednostek pola: \(\textrm{mm}^2\) , \(\textrm{cm}^2\) , \(\textrm{dm}^2\), \(\textrm{m}^2\) , \(\textrm{km}^2\) , \(\textrm{ar}\), \(\textrm{ha}\) (bez zamiany jednostek w trakcie obliczeń).
- 5. Obliczanie pól wielokątów metodą podziału na mniejsze wielokąty lub uzupełniania do większych wielokątów jak w sytuacjach:
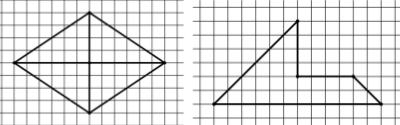
- 6. Obliczanie objętości i pola powierzchni prostopadłościanu przy danych długościach krawędzi.
- 7. Stosowanie jednostek objętości i pojemności: \(\textrm{cm}^3\), \(\textrm{dm}^3\), \(\textrm{m}^3\), \(\textrm{mL}\), \(\textrm{L}\).
-
+ XII. Obliczenia praktyczne.
- 1. Interpretacja 100% danej wielkości jako całości, 50% – jako połowy, 25% - jako jedną czwartą, 10% – jako jedną dziesiątą, 1% – jako jedną setną części danej wielkości liczbowej.
- 2. Obliczanie procentu danej wielkości w stopniu trudności typu 50%, 20%, 10%.
- 3. Proste obliczenia zegarowe na godzinach, minutach i sekundach.
- 4. Proste obliczenia kalendarzowe na dniach, tygodniach, miesiącach, latach.
- 5. Odczytywanie temperatury (dodatniej i ujemnej).
- 6. Zamiana i prawidłowe stosowanie jednostek długości: mm, cm, dcm, m, km.
- 7. Zamiana i prawidłowe stosowanie jednostek masy: g, dag, kg, t.
- 8. Obliczanie rzeczywistej długości odcinka, gdy dana jest jego długość w skali oraz długość odcinka w skali, gdy dana jest jego rzeczywista długość.
- 9. Obliczanie przebytej drogi przy danej prędkości i czasie, prędkości przy danej przebytej drodze i czasie, czasu przy danej drodze i prędkości oraz stosowanie jednostki prędkości km/h i m/s.
-
+ XIII. Elementy statystyki opisowej.
- 1. Gromadzenie i porządkowanie danych.
- 2. Odczytywanie i interpretuja danych przedstawionych w tekstach, tabelach, na diagramach i na wykresach, np.: wartości z wykresu, wartość największą, najmniejszą, opisywanie przedstawionego w tekstach, tabelach, na diagramach i na wykresach zjawiska przez określenie przebiegu zmiany wartości danych, np. z użyciem określenia "wartości rosną", "wartości maleją", "wartości są takie same" ("przyjmowana wartość jest stała").
-
+ XIV. Zadania tekstowe.
- 1. Czytanie ze zrozumieniem tekstu z informacjami liczbowymi.
- 2. Wykonywanie wstępnych czynności ułatwiających rozwiązanie zadania, w tym rysunku pomocniczego lub wygodnego zapisania informacji i danych z treści zadania.
- 3. Dostrzeganie zależności między podanymi informacjami.
- 4. Dzielenie rozwiązania zadania na etapy, stosując własne, poprawne, wygodne dla siebie strategie rozwiązania.
- 5. Stosowanie poznanej wiedzy z zakresu arytmetyki i geometrii oraz nabytych umiejętności rachunkowych, a także własnych
poprawnych metod do rozwiązywania zadań osadzonych w kontekście praktycznym.
- 6. Umiejętność weryfikacji wyniku zadania tekstowego, ocena sensowności rozwiązania, np. poprzez szacowanie, sprawdzanie wszystkich warunków zadania, ocenianie rzędu wielkości otrzymanego wyniku.
- 7. Umiejętność układania zadań i łamigłówek, i rozwiązywania ich; stawianie nowych pytań związanych z sytuacją w rozwiązanym zadaniu.
-
+ Klasy VII – VIII
-
+ I. Potęgi o podstawach wymiernych.
- 1. Zapis iloczynu jednakowych czynników w postaci potęgi o wykładniku całkowitym dodatnim.
- 2. Mnożenie i dzielenie potęg o wykładnikach całkowitych dodatnich.
- 3. Mnożenie potęg o różnych podstawach i jednakowych wykładnikach.
- 4. Podnoszenie potęgi do potęgi.
- 5. Odczytywanie i zapis liczby w notacji wykładniczej \( a \cdot 10^k \), gdy \( 1 \leq a < 10 \), k jest liczbą całkowitą.
-
+ II. Pierwiastki.
- 1. Obliczanie wartości pierwiastków kwadratowych i sześciennych z liczb, które są odpowiednio kwadratami lub sześcianami liczb wymiernych.
- 2. Szacowanie wielkości danego pierwiastka kwadratowego lub sześciennego oraz wyrażenia arytmetycznego zawierającego pierwiastki.
- 3. Porównywanie wartości wyrażenia arytmetycznego zawierającego pierwiastki z daną liczbą wymierną oraz znajdowanie liczb wymiernych większych lub mniejszych od takiej wartości, np. znajdowanie liczby całkowitej a takiej, że \( a \leq \sqrt{137} < a+1 \).
- 4. Obliczanie pierwiastka z iloczynu i ilorazu dwóch liczb, wyłączanie liczby przed znak pierwiastka i włączanie liczby pod znak pierwiastka.
- 5. Mnożenie i dzielenie pierwiastków tego samego stopnia.
-
+ III. Tworzenie wyrażeń algebraicznych z jedną i wieloma zmiennymi.
- 1. Zapisywanie wyniku podanych działań w postaci wyrażeń algebraicznych jednej lub kilku zmiennych.
- 2. Obliczanie wartości liczbowej wyrażeń algebraicznych.
- 3. Zapisywanie zależności przedstawionych w zadaniach w postaci wyrażeń algebraicznych jednej lub kilku zmiennych.
- 4. Zapisywanie rozwiązania zadań w postaci wyrażeń algebraicznych jak w przykładzie: Bartek i Grześ zbierali kasztany. Bartek zebrał n kasztanów, Grześ zebrał 7 razy więcej. Następnie Grześ w drodze do domu zgubił 10 kasztanów, a połowę pozostałych oddał Bartkowi. Ile kasztanów ma teraz Bartek, a ile ma Grześ?
-
+ IV. Przekształcanie wyrażeń algebraicznych. Sumy algebraiczne i działania na nich.
- 1. Porządkowanie jednomianów i dodawanie jednomianów podobnych (tzn. różniących się jedynie współczynnikiem liczbowym).
- 2. Dodawanie i odejmowanie sum algebraicznych, redukując wyrazy podobne.
- 3. Mnożenie sum algebraicznych przez jednomian i dodawanie wyrażeń powstałych z mnożenia sum algebraicznych przez jednomiany.
- 4. Mnożenie dwumianu przez dwumian i redukcja wyrazów podobnych.
-
+ V. Obliczenia procentowe.
- 1. Przedstawianie części wielkości jako procent tej wielkości.
- 2. Obliczanie liczby a równej p procent danej liczby b.
- 3. Oliczanie, jaki procent danej liczby b stanowi liczba a.
- 4. Obliczanie liczby b, której p procent jest równe a.
- 5. Stosowanie obliczeń procentowych do rozwiązywania problemów w kontekście praktycznym, również w przypadkach dwukrotnych podwyżek lub obniżek danej wielkości.
-
+ VI. Równania z jedną niewiadomą
- 1. Sprawdzenie, czy dana liczba jest rozwiązaniem równania (stopnia pierwszego, drugiego lub trzeciego) z jedną niewiadomą, np. sprawdzenie, które liczby całkowite niedodatnie i większe od \(-8\) są rozwiązaniami równania \( \frac{x^3}{8}+\frac{x^2}{2}=0 \).
- 2. Rozwiązywanie równania pierwszego stopnia z jedną niewiadomą metodą równań równoważnych.
- 3. Rozwiązywanie równań, które po prostych przekształceniach wyrażeń algebraicznych sprowadzają się do równań pierwszego stopnia z jedną niewiadomą.
- 4. Rozwiązywanie zadań tekstowych za pomocą równań pierwszego stopnia z jedną niewiadomą, w tym także z obliczeniami procentowymi.
- 5. Przekształcanie prostych wzorów, aby wyznaczyć zadaną wielkość we wzorach geometrycznych (np. pól figur) i fizycznych (np. dotyczących prędkości, drogi i czasu).
-
+ VII. Proporcjonalność prosta.
- 1. Przykłady wielkości wprost proporcjonalnych.
- 2. Wyznaczanie wartości przyjmowanej przez wielkość wprost proporcjonalną w przypadku konkretnej zależności proporcjonalnej, np. wartość zakupionego towaru w zależności od liczby sztuk towaru.
- 3. Stosowanie podziału proporcjonalnego.
-
+ VIII. Własności figur geometrycznych na płaszczyźnie.
- 1. Znajomość i stosowanie twierdzenia o równości kątów wierzchołkowych (z wykorzystaniem zależności między kątami przyległymi).
- 2. Przedstawianie na płaszczyźnie dwóch prostych w różnych położeniach względem siebie, w szczególności proste prostopadłe i proste równoległe.
- 3. Korzystanie z własności prostych równoległych, w szczególności stosowanie równości kątów odpowiadających i naprzemianległych.
- 4. Znajomość i stosowanie cechy przystawania trójkątów.
- 5. Znajomość nierówności trójkąta \( AB + BC \geq AC \) i wiedza, kiedy zachodzi równość.
- 6. Wykonywanie prostych obliczeń geometrycznych, wykorzystując sumę kątów wewnętrznych trójkąta i własności trójkątów równoramiennych.
- 7. Znajomość i stosowanie w sytuacjach praktycznych twierdzenie Pitagorasa (bez twierdzenia odwrotnego).
- 8. Przeprowadzanie dowodów geometrycznych nie trudniejszych niż w przykładach:
a) Dany jest ostrokątny trójkąt równoramienny \(ABC\), w którym \(AC = BC\). W tym trójkącie poprowadzono wysokość \(AD\). Udowodnij, że kąt \(ACB\) jest dwa razy większy od kąta \(BAD\).
b) Na bokach \(BC\) i \(CD\) prostokąta \(ABCD\) zbudowano, na zewnątrz prostokąta, dwa trójkąty równoboczne \(BCE\) i \(CDF\). Udowodnij, że \(AE = AF\).
-
+ IX. Wielokąty.
- 1. Znajomość pojęcia wielokąta foremnego.
- 2 Stosowanie wzorów na pole trójkąta, prostokąta, kwadratu, równoległoboku, rombu, trapezu, a także do wyznaczania długości odcinków w zadaniach nie trudniejszych niż w przykładach:
a) Oblicz najkrótszą wysokość trójkąta prostokątnego o bokach długości: 5 cm, 12 cm i 13 cm.
b) Przekątne rombu \(ABCD\) mają długości \(AC = 8 dm\) i \(BD = 10 dm\). Przekątną \(BD\) rombu
przedłużono do punktu \(E\) w taki sposób, że odcinek \(BE\) jest dwa razy dłuższy od tej przekątnej. Oblicz pole trójkąta \(CDE\). (Zadanie ma dwie odpowiedzi.)
-
+ X. Oś liczbowa. Układ współrzędnych na płaszczyźnie.
- 1. Zaznaczanie na osi liczbowej zbiorów liczb spełniających warunek taki jak \(x \geq 1.5 \) lub taki jak \(x \leq -\frac{4}{7}\).
- 2. Znajdowanie współrzędnych danych (na rysunku) punktów kratowych w układzie współrzędnych na płaszczyźnie.
- 3. Rysowanie w układzie współrzędnych na płaszczyźnie punktów kratowych o danych współrzędnych całkowitych (dowolnego znaku).
- 4. Znajdowanie środka odcinka, którego końce mają dane współrzędne (całkowite lub wymierne) oraz znajdowanie współrzędnych drugiego końca odcinka, gdy dany jest jeden koniec i środek.
- 5. Obliczanie długości odcinka, którego końce są danymi punktami kratowymi w układzie współrzędnych.
- 6. Dla danych punktów kratowych A i B znlezienie innych punktów kratowych należących do prostej AB.
-
+ XI. Geometria przestrzenna.
- 1. Rozpoznawanie graniastosłupów i ostrosłupów – w tym prostych i prawidłowych.
- 2. Obliczanie objętości i pola powierzchni graniastosłupów prostych, prawidłowych i takich, które nie są prawidłowe o poziomie trudności nie większym niż w przykładowym zadaniu:
Podstawą graniastosłupa prostego jest trójkąt równoramienny, którego dwa kąty mają miarę po 45°, a najdłuższy bok ma długość \( 6 \sqrt{2} \textrm{dm} \) . Jeden z boków prostokąta, który jest w tym graniastosłupie ścianą boczną o największej powierzchni, ma długość \(4 \textrm{dm}\) . Oblicz objętość i pole powierzchni całkowitej tego graniastosłupa.
- 3. Obliczanie objętości ostrosłupów i pola powierzchni ostrosłupów prawidłowych, i takich, które nie są prawidłowe w zadaniach nie trudniejszych niż w przykładzie:
Prostokąt \(ABCD\) jest podstawą ostrosłupa \(ABCDS\), punkt \(M\) jest środkiem krawędzi \(AD\),
odcinek \(MS\) jest wysokością ostrosłupa. Dane są następujące długości krawędzi:
\(AD = 10 \textrm{cm}\), \(AS = \textrm{13 cm}\) oraz \(AB = \textrm{20 cm}\).
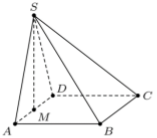
Oblicz objętość ostrosłupa.
-
+ XII. Wprowadzenie do kombinatoryki i rachunku prawdopodobieństwa.
- 1. Wyznaczanie zbiorów obiektów, analiza i obliczanie, ile jest obiektów, mających daną własność, w przypadkach niewymagających stosowania reguł mnożenia i dodawania.
- 2. Przeprowadzanie prostych doświadczeń losowych, polegających na rzucie monetą, rzucie sześcienną kostką do gry, rzucie kostką wielościenną lub losowaniu kuli spośród zestawu kul, analizowanie ich i obliczanie prawdopodobieństwa zdarzeń w doświadczeniach losowych.
-
+ XIII. Odczytywanie danych i elementy statystyki opisowej.
- 1. Interpretacja danych przedstawionych za pomocą tabel, diagramów słupkowych i kołowych, wykresów, w tym także wykresów w układzie współrzędnych.
- 2. Tworzenie diagramów słupkowych i kołowych oraz wykresów liniowych na podstawie zebranych przez siebie danych lub danych pochodzących z różnych źródeł.
- 3. Obliczanie średniej arytmetycznej kilku liczb.
-
+ XIV. Długość okręgu i pole koła.
- 1. Obliczanie długości okręgu o danym promieniu lub danej średnicy.
- 2. Obliczanie promienia lub średnicy okręgu o danej długości okręgu.
- 3. Obliczanie pola koła o danym promieniu lub danej średnicy.
- 4. Obliczanie promienia lub średnicy koła o danym polu.
-
+ XV. Symetrie.
- 1. Rozpoznawanie symetralnej odcinka i dwusiecznej kąta.
- 2. Znajomość i stosowanie w zadaniach podstawowych własności symetralnej odcinka i dwusiecznej kąta jak w przykładzie:
Wierzchołek \(C\) rombu \(ABCD\) leży na symetralnych boków \(AB\) i \(AD\). Oblicz miary kątów tego rombu.
- 3. Rozpoznawanie figur osiowosymetrycznych i wskazywanie ich osi symetrii oraz uzupełnianie figury do figury osiowosymetrycznej przy danych: osi symetrii figury i części figury.
- 4. Rozpoznawanie figur środkowosymetrycznych i wskazywanie ich środków symetrii.
 axplusb.pl
axplusb.pl
